Mapa potenciométrico utilizando R

Curso de Análise Espacial e Interpolação de Dados no R

Dias 09 a 13 de Junho, das 19h as 21h

Inscrições abertas, vagas limitadas.

https://geosaber.com.br

1. Carregar e preparar dados

library(gstat)
library(terra)
library(tidyterra)
library(sf)
library(sp)
library(ggplot2)
library(ggspatial)
library(dplyr)
library(purrr)
library(tidyr)

data(meuse, package = "sp")
meuse_sf <- st_as_sf(meuse, coords = c("x", "y"), crs = 28992)  # RD New

# ------------------------------------------
# 1. Criar grid de interpolação
# ------------------------------------------
bbox <- st_bbox(meuse_sf)
grid <- rast(
  ext(bbox[c("xmin", "xmax", "ymin", "ymax")]),
  resolution = 10,  # 10m de resolução
  crs = "EPSG:28992"
)

2. Superfície Potenciométrica

# ------------------------------------------
# 2. Análise geoestatística
# ------------------------------------------
# Variograma experimental
vario <- variogram(elev ~ 1, meuse_sf)

# Ajustar modelo
modelo <- fit.variogram(vario, vgm("Gau"))  # Modelo exponencial

# Visualizar ajuste
plot(vario, model = modelo, main = "Modelo de Variograma")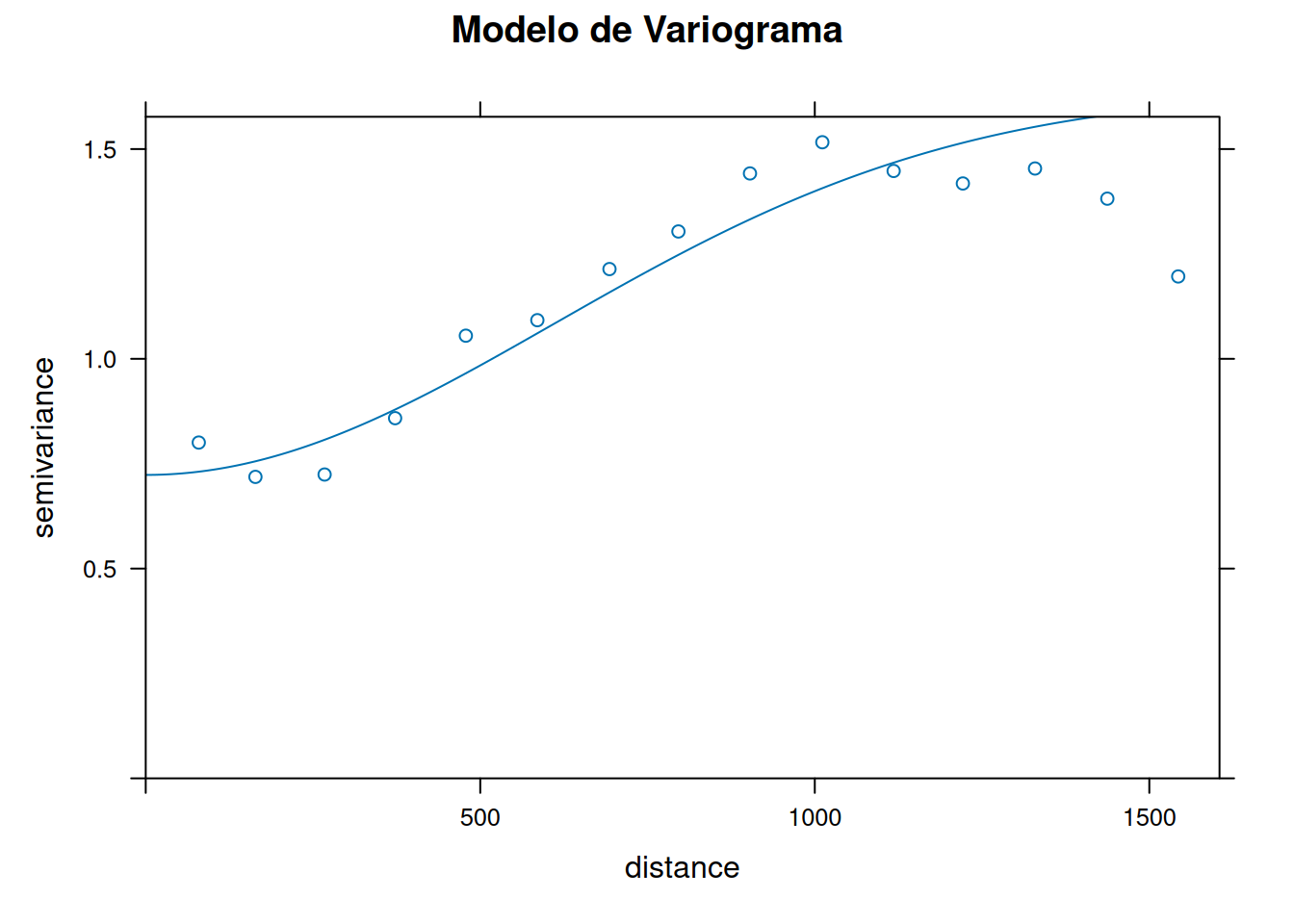

# ------------------------------------------
# 3. Krigagem Ordinária
# ------------------------------------------
krige_result <- krige(
  elev ~ 1,
  meuse_sf,
  st_as_sf(as.points(grid)),  # Converter raster para pontos
  model = modelo
)
[using ordinary kriging]
# ------------------------------------------
# 4. Converter para raster
# ------------------------------------------
elev_raster <- rast(grid)
values(elev_raster) <- krige_result$var1.pred
names(elev_raster) <- "Elevação"

# ------------------------------------------
# 5. Visualização
# ------------------------------------------
# Mapa de elevação
plot(elev_raster, col = terrain.colors(100), main = "Superfície Potenciométrica")

# Sobrepor pontos originais
plot(st_geometry(meuse_sf), add = TRUE, pch = 20, cex = 0.8)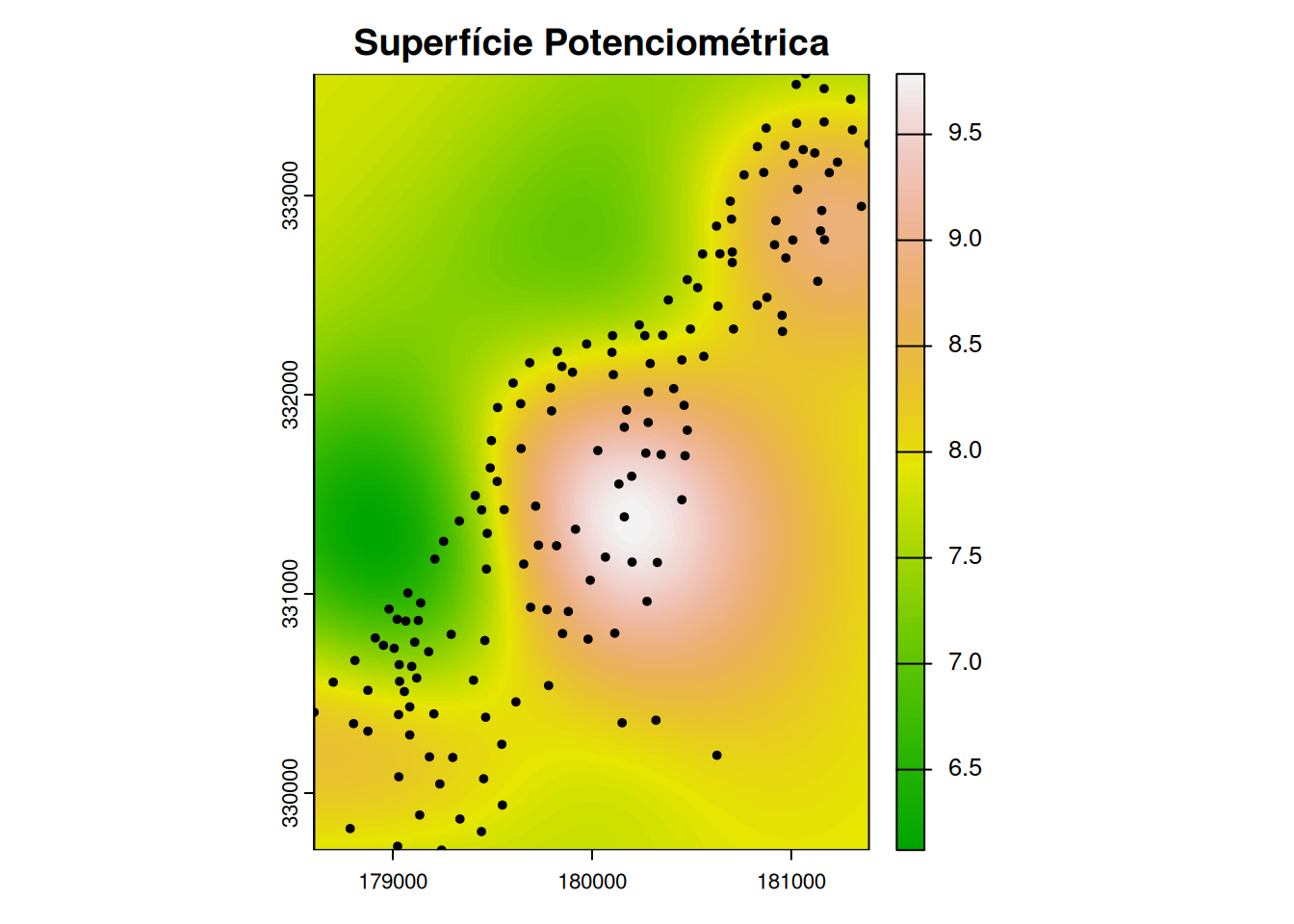

# ------------------------------------------
# 6. Validação Cruzada (Opcional)
# ------------------------------------------
krige_cv <- krige.cv(elev ~ 1, meuse_sf, model = modelo)
print(paste("RMSE:", round(sqrt(mean(krige_cv$residual^2)), 2), "metros"))
[1] "RMSE: 0.8 metros"

3. Cálculo do Gradiente Hidráulico

# Calcular componentes do gradiente (direção do fluxo)
gradient <- terrain(elev_raster, v = c("slope", "aspect"), unit = "radians")

# Componentes do vetor gradiente (PERPENDICULAR às isolinhas)
dx_rast <- sin(gradient$aspect) * gradient$slope  # Componente x
dy_rast <- cos(gradient$aspect) * gradient$slope   # Componente y

4. Geração das Setas de Fluxo

arrow_grid <- st_make_grid(meuse_sf, cellsize = 350, what = "centers") %>% 
  st_as_sf() %>% 
  vect()

# Extração e normalização dos vetores
arrow_data <- data.frame(
  x = crds(arrow_grid)[,1],
  y = crds(arrow_grid)[,2],
  dx = as.numeric(terra::extract(dx_rast, arrow_grid)[,2]),
  dy = as.numeric(terra::extract(dy_rast, arrow_grid)[,2])
) %>% 
  filter(!is.na(dx) & !is.na(dy)) %>%
  mutate(
    # Normalização para tamanho fixo (mantendo direção)
    norm = sqrt(dx^2 + dy^2),
    dx_norm = dx/norm * 200,  # 50 = comprimento fixo
    dy_norm = dy/norm * 200,
    xend = x + dx_norm,
    yend = y + dy_norm
  )

5. Visualização Final

library(ggplot2)
ggplot() +
  # Mapa de potencial
  geom_spatraster(data = elev_raster) +
  scale_fill_viridis_c(option = "viridis", name = "Potencial (m)") +
  
  # Linhas equipotenciais
  geom_spatraster_contour(
    data = elev_raster,
    breaks = seq(floor(min(values(elev_raster), na.rm = TRUE)),
             ceiling(max(values(elev_raster), na.rm = TRUE)), 
             by = 1),
    color = "white",
    alpha = 0.5,
    linewidth = 0.3
  ) +
  
  # Vetores de fluxo (setas)
  geom_segment(
    data = arrow_data,
    aes(x = x, y = y, xend = xend, yend = yend),
    color = "red",
    linewidth = 0.6,
    arrow = arrow(
      angle = 20,
      length = unit(0.1, "inches"),
      type = "open"
    )
  ) +
  
  # Elementos cartográficos
  annotation_scale(location = "br") +
  annotation_north_arrow(
    location = "tr",
    which_north = "true",
    style = north_arrow_minimal()
  ) +
  
  # Formatação
  labs(title = "Mapa Potenciométrico com Linhas de Fluxo",
       subtitle = "Setas indicam direção do gradiente hidráulico") +
  theme_minimal() +
  theme(
    panel.background = element_rect(fill = "lightblue", color = NA),
    legend.position = "right"
  ) +
  coord_sf()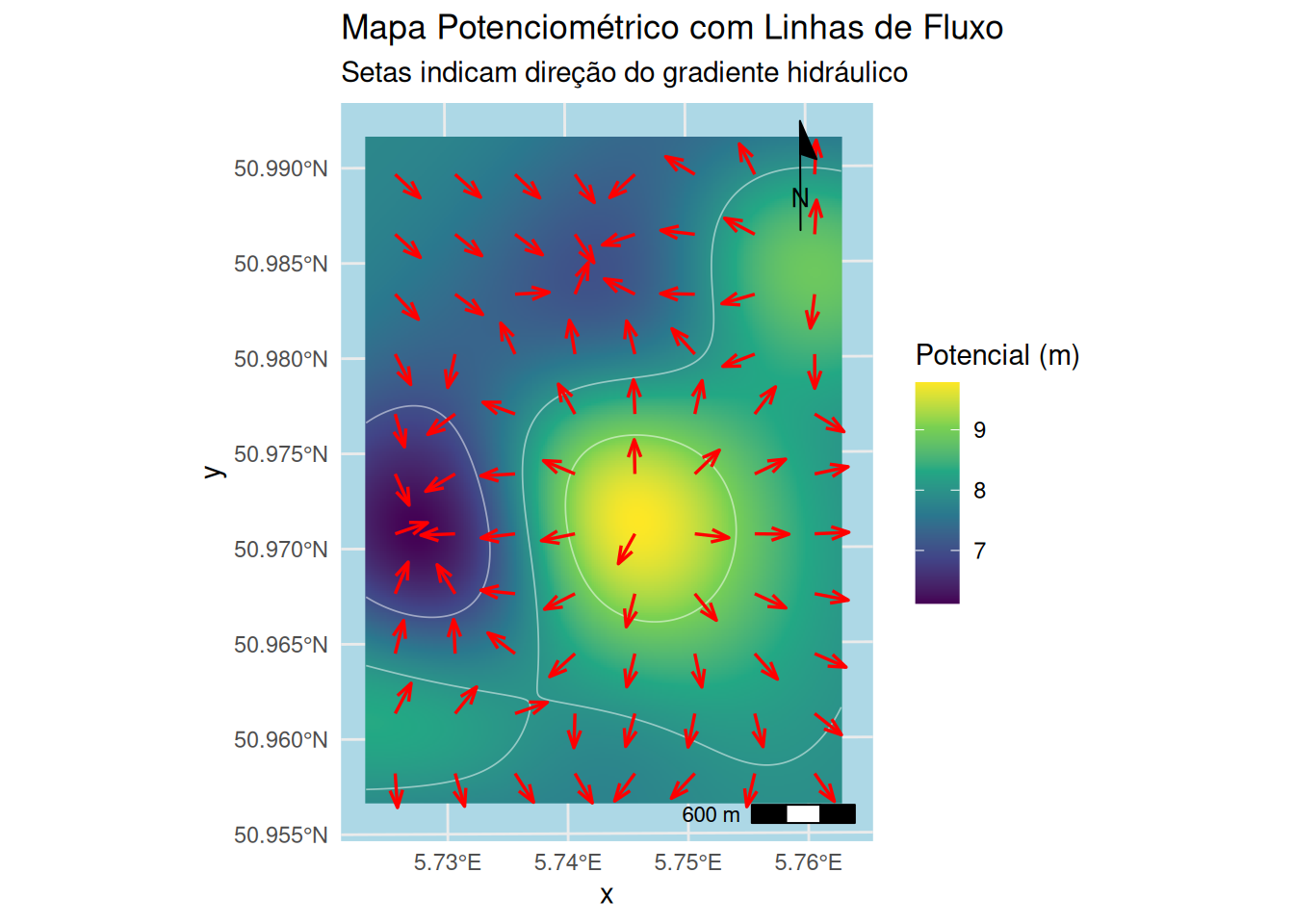

Princípios Científicos Implementados:

  1. Orientação do Gradiente:

    • O cálculo -sin(aspect) e -cos(aspect) garante que as setas apontem de maior para menor potencial
    • Multiplicação pelo slope mantém a relação com a magnitude do gradiente

  2. Normalização Vetorial:

    norm = sqrt(dx^2 + dy^2),
dx_norm = dx/norm * 50,  # Comprimento fixo de 50 unidades
dy_norm = dy/norm * 50
    • Mantém direção original mas com magnitude constante

  3. Perpendicularidade às Isolinhas:

    • O vetor gradiente é por definição perpendicular às linhas equipotenciais
    • A visualização com geom_segment() preserva esta relação geométrica

Parâmetros Ajustáveis:

  • Densidade das setas: Modificar cellsize em st_make_grid()
  • Comprimento das setas: Ajustar o multiplicador 50 na normalização
  • Estilo visual: Alterar cores, espessuras e tipos de seta

Esta solução produz um mapa hidrogeologicamente correto, com:

✓ Setas perpendiculares às isolinhas

✓ Direção consistente com o gradiente potencial

✓ Tamanho uniforme para melhor legibilidade

✓ Elementos cartográficos profissionais